Infinity: You Can't Get There from Here

Introduction

Every child becomes aware of infinity when he or she learns to count. We all went through this, and for most of us it snuck up on us gradually. This is because we weren’t expected to count very high at first. Getting to “three” was perhaps our first achievement in breaking into the world of “many’s.” Then it turned out there was something called “ten,” and it took a little time to work out precisely how to get there from “three.” Once that was mastered we might have been expected to rest on our laurels—but it was not to be. For there was an “eleven.” And a “twelve.” And then, for crying out loud, all those “‘teens!” By now a sneaking suspicion had begun to break across our awareness, and we wanted to ask, “when does this end?” And then, dreadfully, “does it end?” And at last the awful truth: it NEVER ends.

Fortunately, after “twenty” it all breaks down to a pretty simple system and the rest is easy. We turned our attention, gratefully, to other things. Still though, the fact that it never ends remained psychologically vexing for most of us. All children try at some point to see how high they can count, even having contests about it. Perhaps this activity is born at least in part of the felt need to challenge this notion of endlessness—to see if it really holds up to experiment. “Infinity,” we called it, and used the word cheerfully whenever we needed it.

“You’re a dumby, nyah nyah!”
“Oh yeah? Well you’re twice as dumb!”
“Well…you’re a hundred times as dumb!”
“Well you’re a million times…”
“Well you’re infinity times …”

…to the last of which a good answer was hard to find. How could you get bigger than infinity? Infinity plus one? And what’s that?

Infinity infected our imaginations, and for some of us it cropped up in our conscious thoughts every now and then in new and interesting ways. I had nightmares for years in which I would think of something doubling in size. And then doubling again. And then doubling again. And then doubling again. And then…until my ability to conceive of it was overwhelmed, and I woke up in a highly anxious state.

Another form this dream took was “something inside of something,” and then all of that inside something else, and all of that inside something else, and…and then I was awake, wide-eyed and perspiring. Only when I studied mathematics did I discover that my dream contained the seed of an important idea, an idea that the mathematician John Von Neumann had years before developed quite consciously and deliberately. It is called the Von Neumann heirarchy, and it is a construction in set theory.

There are many ways infinity can catch our imagination. Everyone has wondered if the universe is infinite, for instance. It is an easy mistake to conclude that it must be, reasoning that if it weren’t then it would have to have a boundary, and then what would be on the other side? The answer to this is that the universe may be like a sphere. The surface of a sphere doesn’t have a boundary, but it is certainly finite in area. (The universe, in other words, could be like a three-dimensional surface of a sphere which can be imagined as existing in four-dimensional space—most cosmologists think it may well be something like that.) Another common line of thought runs like this: if the universe is infinite then it must have an infinite number of planets, and therefore a planet just like this one except that everyone is bald (or talks backwards, or what have you).

The trouble here is in thinking that an infinite set must contain everything. However, a little thought shows that this needn’t be true. For instance, if I have an infinite set of natural numbers, must it contain the number 17? Obviously not; there are infinitely many even numbers, yet the set of even numbers doesn’t contain the number 17. (Indeed, there are infinitely many infinite sets of natural numbers that don’t contain the number 17!)

Infinities don’t have to be large, of course—they can also be small. Instead of something doubling in size, it could be halved. And then halved again. And then halved again. And then halved again. And then…and so on forever. This is the basis of Zeno’s Paradox of the Tortoise and Achilles, in which it is proved that motion is impossible. There are other ways of thinking of infinity, too. A circle is infinite, in the sense that one can go round it forever, and many Hindus believe that all of creation is a great circle that repeats itself endlessly. And who hasn’t stood between two mirrors? What other kinds of infinity can you think of?

*2*

The History of Infinity

It is a surprising fact that throughout most of the history of mathematics infinity was a taboo subject. Mathematicians just didn’t like to talk about it. There were many reasons for this, but a good deal of it goes right back to Aristotle. A student of Plato’s and a tutor of Alexander the Great, Aristotle has been considered the most widely learned scholar of all time. He wrote extensively on philosophy, logic, and natural science, and his ideas held great authority long after the end of the classical period. During the middle ages his teachings formed the foundation of almost all formal learning. His views on infinity are summed up in this passage from Book III of his monumental work Physics,

Since no sensible magnitude is infinite, it is impossible to exceed every assigned magnitude; for if it were possible there would be something bigger than the heavens.

Aristotle distinguished between the potential infinite and the actual infinite. The natural numbers, he would say, are potentially infinite because they have no greatest member. However, he would not allow that they are actually infinite, as he believed it impossible to imagine the entire collection of natural numbers as a completed thing. He taught that only the potential infinite is permissible to thought, since any notion of the actual infinite is not “sensible.” So great was Aristotle’s influence that more than 2,000 years later we find the great mathematician Karl Friederich Gauss admonishing a colleague in 1831,

As to your proof, I must protest most vehemently against your use of the infinite as something consummated, as this is never permitted in mathematics. The infinite is but a figure of speech….

Nonetheless, long before Gauss’s time, cracks had begun to appear in the Aristotelian doctrine. Galileo (b. 1564) had given the matter much thought and noticed the following curious fact: if you take the set of natural numbers and remove exactly half of them, the remainder is as large a set as it was before. This can be seen, for example, by removing all the odd numbers from the set, so that only the even numbers remain. By then pairing every natural number n with the even number 2n, we see that the set of even numbers is equinumerous with the set of all natural numbers. Galileo had hit upon the very principle by which mathematicians in our day actually define the notion of infinite set, but to him it was too outlandish a result to warrant further study. He considered it a paradox, and “Galileo’s Paradox” it has been called ever since.

As the modern study of mathematics came into full bloom during the seventeenth and eighteenth centuries, more and more mathematicians began to sneak the notion of an actual infinity into their arguments, occasionally provoking a backlash from more rigorous colleagues (like Gauss).

In the 1660’s Isaac Newton in England and Gottfried Leibnitz in Germany (working independently) began their development of the calculus, which involved techniques that all but demanded the admission of actual infinities. Newton side-stepped the issue by introducing an obscure notion called “fluxions,” the precise nature of which was never made clear. Later he changed the terminology to “the ultimate ratio of evanescent increments.”

The discovery of the calculus opened the way to the study of mathematical analysis, in which the issue of actual infinities becomes very difficult indeed to avoid. All through the nineteenth century mathematicians struggled to preserve the Aristotelian doctrine, while still finding ways to justify the marvelous discoveries which their investigations forced upon them.

Finally, in the early 1870’s, an ambitious young Russian/German mathematician named Georg Cantor upset the applecart completely. He had been studying the nature of something called trigonometric series and had already published two papers on the topic. His results, however, depended heavily on certain assumptions about the nature of real numbers. Cantor pursued these ideas further, publishing, in 1874, a paper titled, On a Property of the System of all the Real Algebraic Numbers. With this paper the field of set theory was born, and mathematics was changed forever. Cantor completely contradicted the Aristotelian doctrine proscribing actual, “completed” infinities, and for his boldness he was rewarded with a lifetime of controversy, including condemnation by many of the most influential mathematicians of his time. This reaction stifled his career and may ultimately have destroyed his mental health. It also, however, gained him a prominent and respected place in the history of mathematics, for his ideas were ultimately vindicated, and they now form the very foundation of contemporary mathematics.

*3*

Cantor’s Set Theory

Georg Cantor’s discoveries in set theory rest upon a very simple idea, an idea which may be illustrated in the following way. Suppose you couldn’t count to five. That’s difficult to imagine, I admit—but then for each of us there was a time when this was actually true! So go ahead, imagine it.

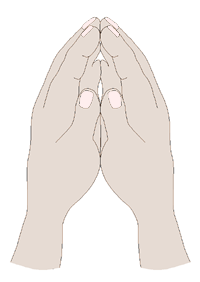
Now look at your hands. If your were unable to count to five, how would you know there are the same number of fingers on each hand? You couldn’t count the fingers on one hand and then count the fingers on the other hand, to see that there were the same number of fingers on each, because you couldn’t count that high. What could you do? The answer is simple: place the thumb of your right hand against the thumb of your left hand. Then place your index fingers together, and then all the other fingers in a one-to-one match-up. When you are done, each finger of each hand is matched to the corresponding finger of the other hand, with none left over on either side. You still don’t know how many fingers are on each hand, but you do know that they are the same number.

Now, the real trouble with infinity is much the same: we can’t count that high! Cantor’s insight was that even though we can’t enumerate an infinite set we can nonetheless apply the same procedure to any well-defined infinite set that we applied above to determining if our hands have the same number of fingers. In other words, we can determine if two infinite sets are the same “size” (equinumerous) by seeking to find a one-to-one match-up between the elements of each set. Now, remember Galileo’s Paradox? Galileo noticed that we can do the following:

Thus, we can assign each number n in the set of natural numbers to the corresponding number 2n in the set of even numbers. This rule specifies a one-to-one match-up between the set of all natural numbers and the set of even natural numbers. By definition, then, these sets are equinumerous—the same size. We can play the same game with many subsets of the natural numbers. For example, we can form a one-to-one match-up between the natural numbers and the set of squares, or the set of multiples of five, or the set of prime numbers, or the set of numbers greater than 37.

We may feel some discomfort at the idea that we can remove some of the elements of a set and still have as many as we started with, but this is an artifact of our experience with finite sets (in which removing something means having a smaller set). Infinite sets simply don’t behave that way. In fact, this leads us to a definition:

Defⁿ: A set is infinite if we can remove some of its elements without reducing its size.

We have a special name for the “size” of a set: cardinality. We say that the set of natural numbers and the set of even numbers, for instance, have the same cardinality. Also, whenever a set has the same cardinality as the natural numbers, we say that the set in question is countable, since it can be put into a one-to-one correspondence with the counting numbers (i.e., the set of natural numbers).

Cantor’s next great accomplishment was to ask the question, “do all infinite sets have the same cardinality?” In other words, can all infinite sets be put into a one-to-one match-up with the natural numbers? It is not difficult to find one-to-one matchups between the natural numbers and the integers (you should try to do this), so the first set to consider as—possibly—cardinally larger is the set of rational number. Recall that the rational numbers are dense, which means that between any two rational numbers on the real number line we can find infinitely more rational numbers. This suggests to our intuition that the set of rational numbers may be, in some sense, “bigger” than the set of natural numbers. However, it turns out that the rational numbers are indeed countable, as may be seen by examining the following table:

This table, if completed down and across (an infinite process!) contains all the rational numbers. (It contains many duplications, of course. All the fractions on the main diagonal, for instance, are really just the same number—one—but that won’t affect our argument.) Now, we can “count” the rational numbers by just following the criss-crossing line. Thus, the rational numbers really are countable—that is, there are just as many natural numbers as there are rational numbers. Given how the set of rational numbers seems to contain infinities within infinities, this is an astounding result.

The next set to ask about, obviously, is the real numbers. After our experience with the rational numbers it would be understandable to guess that, after all, countable infinities are the only kind of infinities there are in mathematics. But no! Cantor showed that the real numbers are cardinally larger than the natural numbers—in other words, there is no way to form a one-to-one match-up between the natural numbers and the real numbers that doesn’t leave some of the real numbers out. To show this, Cantor invented a whole new kind of proof that has come to be called “Cantor’s diagonalization argument.”

Cantor’s proof of the “nondenumerability” of the real numbers (the diagonalization argument) is somewhat more sophisticated than the proofs we have examined hitherto. However, laying aside some purely technical matters, we can provide a simplified—but still convincing—version of his proof in the following way. Remember that we are attempting to prove a negative statement: that the real numbers are not countable. As so often in such cases, we approach this issue through the back door, so to speak, with a proof by contradiction. In other words, we begin by assuming, for sake of argument, that the real numbers are countable. This would mean that we could form a one-to-one matchup of the natural numbers and the real numbers. Since real numbers may be represented in decimal form (with an integer part and a decimal part), this means that we could provide a numbered list of the real numbers which would look something like this:

…where the numbers on the left are the natural numbers, and the numbers on the right are a “denumeration” of the real numbers. That is, we are supposing that we eventually have every real number running down the right-hand side of this list, with its corresponding natural number next to it. Now, Cantor concluded that there exists at least one real number that can’t be on the list, and he reasoned as follows: Create a new real number by first picking any number for the integer part (zero will do), and then let its first decimal place digit be different from the digit in the first decimal place in the first number in our list. Then let our new number’s second decimal place digit be different from the digit in the second decimal place in the second real number in our list. Proceed in the same way, so that each decimal place digit in our new number is different from the corresponding digit in the corresponding real number in the list. Thus, we could do somthing like the following:

Now we ask the question, is our new real number on the list? Well, it can’t be the same as the first number on the list since it is different in the first decimal place, owing to the way we constructed it. Likewise, it can’t be the same as the second number on the list since it is different from that one in the second decimal place. In fact, we see that it can’t be the same as any of the real numbers in our list, since it differs from each number on the list in at least one decimal place.

BUT—we assumed we had a complete list. This is a contradiction. Therefore, our assumption that we could make a countable list of the real numbers is false! The real numbers have a higher order of infinity than the natural numbers, i.e., they are cardinally greater. (It is natural to ask, “well, why not just add the new number to the list?” Indeed, we could do so. However, this fails to address the fundamental point of the argument: we assumed we had a complete list of real numbers, and then showed that this assumption cannot be true. It is the existence of this contradiction which forces the conclusion that the real numbers aren’t countable. And of course, even if we added our new one to the list, we could use the same process to create infinitely more. There’s just no way to create a completed match-up between the sets.)

*4*

Cardinals

Now that we have two cardinalities—the countable cardinality of the natural numbers and the uncountable cardinality of the real numbers—we have the beginnings of a collection (a set!) of “cardinalities.” We’ll call them cardinal numbers and give them symbols to stand for them. Following tradition, let us denote the natural numbers—considered as a completed set— by the lower-case Greek letter \(\omega\) (omega), and we’ll say that any other set that can be put into a one-to-one correspondence with the natural numbers has “the size of \(\omega\).” We’ll denote the cardinality of the real numbers by a lower-case c, which stands for continuum.

Now our set of cardinal numbers contains only two elements, but let’s make an adjustment at once. Since cardinal numbers are used to describe the “sizes” of sets, it happens that we really want to call the natural numbers “cardinal numbers” too. After all, they describe the sizes of finite sets. And we may as well have zero, since that’s the size of the empty set. Thus, the set of all cardinals will contain both kinds of cardinal; finite cardinals (which are just the natural numbers, really, together with zero) and what Cantor termed transfinite cardinals, which include those the size of \(\omega\) and c.

\[\mbox{cardinals }=\{1, 2, 3, \ldots, \omega, c, \ldots \mbox{?}\}\]

Notice the question mark. We haven’t really settled whether there are any more transfinite cardinals. Fortunately, Cantor has done that for us, in what is now called Cantor’s Theorem. It may be stated as follows.

Th^m: (Cantor’s Theorem) If X is any set, then there exists at least one set, the power set of X, that is cardinally larger than X.

The proof of Cantor’s Theorem has a similar flavor to his proof of the nondenumerability of the real numbers, but it is somewhat more abstract. The intrepid will have little difficulty following it, however (see Cantor’s Theorem in the Encyclopedia). It is an interesting fact that the power set of any countable set, i.e., of the size of \(\omega\), has the cardinality of c, i.e., of the size of the continuum.

What Cantor’s Theorem tells us is that we can construct sets with greater and greater cardinalities. Cantor introduced a special notation for this heirarchy of cardinalities using the Hebrew letter \(\aleph\) (pronounced AH-leff ), with numeral subscripts showing where they are in the heirarchy. Thus, \(\aleph_0\) is the first infinite cardinal, and denotes the cardinality of the natural numbers (or any countably infinite set, i.e. of the size of \(\omega\)), and \(\aleph_1\) is the next cardinal number, standing for the next size of infinity, and so on.

Now we know what to replace the question mark with—since there is no largest cardinality this list goes on forever, with more and more aleph’s denoting larger and larger kinds of infinity. And we know where the \(\omega\) belongs in this list—it is the size of the first infinite cardinal, \(\aleph_0\).

What about c, the continuum? Cantor thought that it must have size \(\aleph_1\), that is, that the size of the continuum was the next highest after the natural numbers. This conjecture is now called the continuum hypothesis. Cantor was never able to prove it, however, and this bothered mathematicians for many years. How could we be sure where the “size” of the real numbers fit in the scheme of things?

In the 1930’s, Kurt Gödel showed that the continuum hypothesis can’t be disproved from the axioms of set theory, and in the 1960’s another mathematician named Paul Cohen showed that it cannot be proved, either. This is a very strange thing, and mathematicians have debated what it means ever since. At the very least it means that our current understanding of sets is not strong enough to settle the question of the continuum. We have, at present, no way of determining where in the heirarchy of infinite cardinals the cardinality of the continuum belongs.

Conclusion

Infinity, as we have seen, is an idea that reaches far beyond that haunting intuition of endlessness which stems from our early childhood experience of number. To a present day mathematician infinity is both a tool for daily use in his or her work, and a vast and intricate landscape demanding to be explored. This article has provided only a bare introduction to the topic of infinity, and there remain many beautiful ideas for the interested reader to discover: infinitesimal numbers, surreal and hyperreal numbers, and transfinite ordinals, to name just a few. Indeed, the possibilities are probably…well, you know!

Contributors

• B. Sidney Smith, author

Citation Info

• [MLA] Smith, B. Sidney. "Infinity: You Can’t Get There From Here." Platonic Realms Minitexts. Platonic Realms, 13 Jun 2013. Web. **TODAY**. <https://platonicrealms.com/>
• [APA] Smith, B. Sidney (13 Jun 2013). Infinity: You Can’t Get There From Here. Retrieved **TODAY** from the Platonic Realms Minitexts: https://platonicrealms.com/minitexts/Infinity-You-Cant-Get-There-From-Here/

All M.C. Escher works and images copyright © Cordon Art B.V., PO Box 101, 3740 AC The Netherlands. Used by permission. M.C. Escher (TM) is a Trademark of Cordon Art B.V. No M.C. Escher image may be produced, reproduced, stored in a retrieval system, or transmitted in any form or by any means—electronic, mechanical, photocopying, recording, or otherwise—without the written permission of the copyright owner. Visit the official Escher site at mcescher.com.